Batch normalization in convolutional neural networks
Batch Normalization in Convolutional Neural Networks
Batch normalization is a term commonly mentioned in the context of convolutional neural networks. In this article, we are going to explore what it actually entails and its effects, if any, on the performance or overall behavior of convolutional neural networks.
1
2
3
4
5
6
7
8
9
10
11
12
13
import torch
import torch.nn as nn
import torch.nn.functional as F
import torchvision
import torchvision.transforms as transforms
import torchvision.datasets as Datasets
from torch.utils.data import Dataset, DataLoader
import numpy as np
import matplotlib.pyplot as plt
import cv2
from tqdm.notebook import tqdm
import seaborn as sns
from torchvision.utils import make_grid
1
2
3
4
5
6
if torch.cuda.is_available():
device = torch.device('cuda:0')
print('Running on the GPU')
else:
device = torch.device('cpu')
print('Running on the CPU')
The Term Normalization
Normalization in statistics refers to the process of constraining data or a set of values between the range of 0 and 1. Rather inconveniently, in some quarters normalization also refers to the process of setting the mean of a distribution of data to zero and its standard deviation to 1.
In actual sense, this process of setting the mean of a distribution to 0 and its standard deviation to 1 is called standardization. Due to certain liberties however, it is also called normalization or z-score normalization. It is important to learn that distinction and bare it in mind.
Data Preprocessing
Data preprocessing refers to the steps taken in preparing data before being fed to a machine learning or deep learning algorithm. The two processes (normalization and standardization) mentioned in the previous section are data preprocessing steps.
Min-max Normalization
Min-max normalization is one of the most common methods of normalizing data. Typical to its name, it constrains data points within the range of 0 and 1 by setting the minimum value in the dataset to 0, the maximum to 1 and everything in between scaled accordingly. The equation below provides a mathematical description of the min-max normalization process. Essentially it involves subtracting the minimum value in the dataset from each data point then dividing by the range (maximum - minimum).

Using the function below we can replicate the process of min-max normalization. Utilizing this function we can develop an intuition for what actually goes on behind the scenes.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def min_max_normalize(data_points: np.array):
"""
This function normalizes data by constraining
data points between the range of 0 & 1
"""
# convert list to numpy array
if type(data_points) == list:
data_points = np.array(data_points)
else:
pass
# create a list to hold normalized data
normalized = []
# derive minimum and maximum values
minimum = data_points.min()
maximum = data_points.max()
# convert to list for iteration
data_points = list(data_points)
# normalizing data
for value in data_points:
normalize = (value-minimum)/(maximum-minimum)
normalized.append(round(normalize, 2))
return np.array(normalized)
Lets create an array of random values using NumPy then attempt to normalize them using the min-max normalization function defined above.
1
2
3
4
5
# creating a random set of data points
data = np.random.rand(50)*20
# normalizing data points
normalized = min_max_normalize(data)
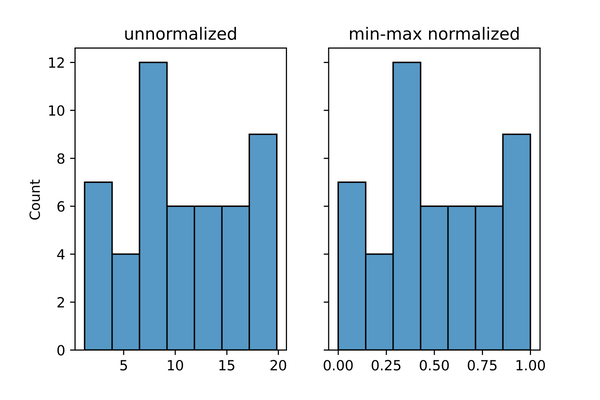
From the plots below, it can be seen that before normalization, values ranged from o to 20 with a vast majority of data points having values between 5 and 10. After normalization however, it can be seen that values now range between 0 and 1 with a vast majority of data points having values between 0.25 and 0.5. Note: if/when you run this code the data distribution will be different from what is used in this article as it is randomly generated.
1
2
3
4
5
6
# visualising distribution
figure, axes = plt.subplots(1, 2, sharey=True, dpi=100)
sns.histplot(data, ax=axes[0])
axes[0].set_title('unnormalized')
sns.histplot(normalized, ax=axes[1])
axes[1].set_title('min-max normalized')
Z-score Normalization
Z-score normalization, also called standardization, is the process of setting the mean and standard deviation of a data distribution to 0 and 1 respectively. The equation below is the mathematical equation which governs z-score normalization, it involves subtracting the mean of the distribution from the value to be normalized before dividing by the distribution’s standard deviation.

The function defined below replicates the z-score normalization process, with this function we can take a closer look at what it actually entails.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def z_score_normalize(data_points: np.array):
"""
This function normalizes data by computing
their z-scores
"""
# convert list to numpy array
if type(data_points) == list:
data_points = np.array(data_points)
else:
pass
# create a list to hold normalized data
normalized = []
# derive mean and and standard deviation
mean = data_points.mean()
std = data_points.std()
# convert to list for iteration
data_points = list(data_points)
# normalizing data
for value in data_points:
normalize = (value-mean)/std
normalized.append(round(normalize, 2))
return np.array(normalized)
Using the data distribution generated in the previous section, let us attempt to normalize the data points using the z-score function.
1
2
3
4
5
6
7
8
9
10
# normalizing data points
z_normalized = z_score_normalize(data)
# check the mean value
z_normalized.mean()
>>>> -0.0006
# check the standard deviation
z_normalized.std()
>>>> 1.0000
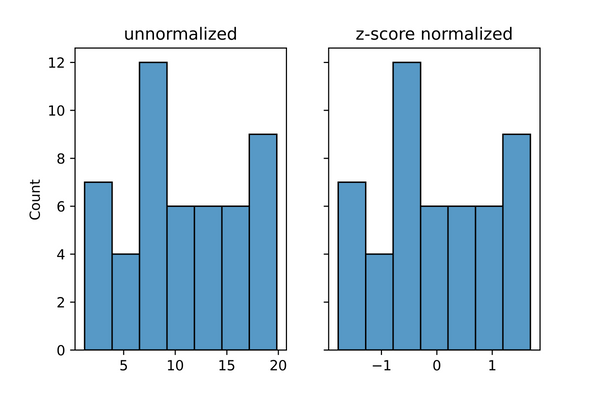
Again, from the visualizations, we can see that the the original distribution has values ranging from 0 to 20 while the z-score normalized values are now centered around 0 (a mean of zero) and a range of approximately -1.5 to 1.5 which is a more manageable range.
1
2
3
4
5
6
# visualizing distributions
figure, axes = plt.subplots(1, 2, sharey=True, dpi=100)
sns.histplot(data, ax=axes[0])
axes[0].set_title('unnormalized')
sns.histplot(z_normalized, ax=axes[1])
axes[1].set_title('z-score normalized')
Reasons for Preprocessing
When regarding data in machine learning, we look at individual data points as features. All of these features are typically not on the same scale scale. For instance, consider a house with 3 bedrooms and a sitting room of size 400 square feet. These two features are on scales so far apart that if they are feed into a machine learning algorithm slated to be optimized by gradient descent. Optimization would be quite tedious, as the feature with the bigger scale will take precedent over all others. In order to ease the optimization process, it is a good idea to have all data points within the same scale.
Normalization in Convolution Layers
The data points in an image are its pixels. Pixel values typically range from 0 to 255; which is why, before feeding images into a convolutional neural network, it is a good idea to normalize them in some way so as to put all pixels in a manageable range.
Even when this is done, when training a convnet, weights (elements in its filters) might become too large, and thereby produce feature maps with pixels spread across a wide range. This essentially renders the normalization done during the preprocessing step somewhat futile. Furthermore, this could hamper the optimization process making it slow or in extreme cases it could lead to a problem called unstable gradients, which could essentially prevent the convnet from further optimizing it’s weights entirely.
In order to prevent this problem, a normalization is introduced in each layer of the convent. This normalization is termed Batch Normalization.
The Process of Batch Normalization
Batch normalization essentially sets the pixels in all feature maps in a convolution layer to a new mean and a new standard deviation. Typically, it starts off by z-score normalizing all pixels, and then goes on to multiply the normalized values by an arbitrary parameter alpha (scale) before adding another arbitrary parameter beta (offset).

These two parameters alpha and beta are learnable parameters which the convnet will then use to ensure that pixel values in the feature maps are within a manageable range - thereby ameliorating the problem of unstable gradients.
Batch Normalization in Action
In order to really assess the effects of batch normalization in convolution layers, we need to benchmark two convnets, one without batch normalization and the other with batch normalization. For this we will be using the LeNet-5 architecture and the MNIST dataset.
Dataset & Convolutional Neural Network Class
In this article, the MNIST dataset will be used for benchmarking purposes as mentioned previously. This dataset consists of 28 x 28 pixel images of handwritten digits ranging from digit 0 to 9 labelled accordingly.
Model without BN
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
class LeNet5(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(1, 6, 5)
self.pool1 = nn.AvgPool2d(2)
self.conv2 = nn.Conv2d(6, 16, 5)
self.pool2 = nn.AvgPool2d(2)
self.linear1 = nn.Linear(5*5*16, 120)
self.linear2 = nn.Linear(120, 84)
self.linear3 = nn. Linear(84, 10)
def forward(self, x):
x = x.view(-1, 1, 32, 32)
#----------
# LAYER 1
#----------
output_1 = self.conv1(x)
output_1 = torch.tanh(output_1)
output_1 = self.pool1(output_1)
#----------
# LAYER 2
#----------
output_2 = self.conv2(output_1)
output_2 = torch.tanh(output_2)
output_2 = self.pool2(output_2)
#----------
# FLATTEN
#----------
output_2 = output_2.view(-1, 5*5*16)
#----------
# LAYER 3
#----------
output_3 = self.linear1(output_2)
output_3 = torch.tanh(output_3)
#----------
# LAYER 4
#----------
output_4 = self.linear2(output_3)
output_4 = torch.tanh(output_4)
#-------------
# OUTPUT LAYER
#-------------
output_5 = self.linear3(output_4)
return(F.softmax(output_5, dim=1))
Batch Normalized LeNet-5

Since the theme of this article is centered around batch normalization in convolution layers, batch norm is only applied on the two convolution layers present in this architecture as illustrated in the image above.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
class LeNet5_BatchNorm(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(1, 6, 5)
self.batchnorm1 = nn.BatchNorm2d(6)
self.pool1 = nn.AvgPool2d(2)
self.conv2 = nn.Conv2d(6, 16, 5)
self.batchnorm2 = nn.BatchNorm2d(16)
self.pool2 = nn.AvgPool2d(2)
self.linear1 = nn.Linear(5*5*16, 120)
self.linear2 = nn.Linear(120, 84)
self.linear3 = nn. Linear(84, 10)
def forward(self, x):
x = x.view(-1, 1, 32, 32)
#----------
# LAYER 1
#----------
output_1 = self.conv1(x)
output_1 = torch.tanh(output_1)
output_1 = self.batchnorm1(output_1)
output_1 = self.pool1(output_1)
#----------
# LAYER 2
#----------
output_2 = self.conv2(output_1)
output_2 = torch.tanh(output_2)
output_2 = self.batchnorm2(output_2)
output_2 = self.pool2(output_2)
#----------
# FLATTEN
#----------
output_2 = output_2.view(-1, 5*5*16)
#----------
# LAYER 3
#----------
output_3 = self.linear1(output_2)
output_3 = torch.tanh(output_3)
#----------
# LAYER 4
#----------
output_4 = self.linear2(output_3)
output_4 = torch.tanh(output_4)
#-------------
# OUTPUT LAYER
#-------------
output_5 = self.linear3(output_4)
return(F.softmax(output_5, dim=1))
Using the code segment below, we can nstantiate model_2 with batch normalization included, and begin training with the same parameters as model_1. Then, we yield accuracy scores..
1
2
3
4
5
# training model 2
model_2 = ConvolutionalNeuralNet(LeNet5_BatchNorm())
log_dict_2 = model_2.train(nn.CrossEntropyLoss(), epochs=10, batch_size=64,
training_set=training_set, validation_set=validation_set)
Looking at the plot, it is clear that both training and validation accuracies increased over the course of training similar to the model without batch normalization. Validation accuracy after the first epoch stood at just above 95%, 3 percentage points higher than model_1 at the same point, before increasing gradually and culminating at approximately 98.5%, 0.5% higher than model_1.
1
2
3
4
5
6
sns.lineplot(y=log_dict_2['training_accuracy_per_epoch'], x=range(len(log_dict_2['training_accuracy_per_epoch'])), label='training')
sns.lineplot(y=log_dict_2['validation_accuracy_per_epoch'], x=range(len(log_dict_2['validation_accuracy_per_epoch'])), label='validation')
plt.xlabel('epoch')
plt.ylabel('accuracy')

Final Remarks
In this article, we explored what normalization entails in a machine learning/deep learning context. We also explored normalization processes as data preprocessing steps and how normalization can be taken beyond preprocessing and into convolution layers via the process of batch normalization.
Afterwards, we examined the process of batch normalization itself before assessing it’s effects by benchmarking two variations of LeNet-5 convnets (one without batch norm and the other with batch norm) on the MNIST dataset. From the results, we inferred that batch normalization contributed to an increase in performance and weight optimization speed. There have also been some suggestions that it prevents internal covariate shift however a concensus might as well not have been reached on that.
Tài liệu tham khảo
Internet
https://lukanguyen.com/articles/translate-batch-normalization-in-3-levels-of-understanding.html
https://blog.paperspace.com/batch-normalization-in-convolutional-neural-networks/
Hết.