Cơ bản về xác suất thống kê
các khái niệm xác suất thống kê
Các khái niệm cơ bản

Bernoulli distribution và categorical distribution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
import numpy as np
class bernoulli():
def pmf(x, p):
# probability mass function
return p**x * (1 - p)**(1 - x)
def mean(p):
# expected value of bernoulli random variable
return p
def var(p):
# variance of bernoulli random variable
return p * (1 - p)
def std(p):
# standart deviation of bernoulli random variable
return bernoulli.var(p)**(1.0/2)
def rvs(p, size = 1):
# random variates
res = np.array([])
for i in range(size):
if np.random.rand() <= p:
res = np.append(res, 1)
else:
res = np.append(res, 0)
return res
p = 0.2
print(bernoulli.mean(p))
print(bernoulli.var(p))
print(bernoulli.std(p))
# each execution generates random number,
print(bernoulli.rvs(p, size = 11))

Univariate và Multivariate normal distribution

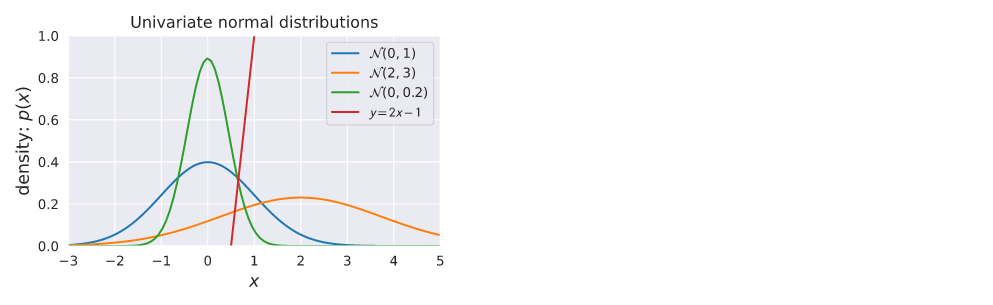
Univariate normal distribution
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
%matplotlib inline
%config InlineBackend.figure_formats = ['svg']
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib import cm
sns.set_style('darkgrid')
np.random.seed(42)
def univariate_normal(x, mean, variance):
return (1.0 / np.sqrt(2 * np.pi * variance)) * np.exp(-(x - mean)**2 / (2 * variance))
# plot
x = np.linspace(-3, 5, num = 100)
y = 2 * x - 1
fig = plt.figure(figsize=(5, 3))
plt.plot(x, univariate_normal(x, mean = 0, variance = 1), label = '$\mathcal{N}(0, 1)$')
plt.plot(x, univariate_normal(x, mean = 2, variance = 3), label = '$\mathcal{N}(2, 3)$')
plt.plot(x, univariate_normal(x, mean = 0, variance = .2), label = '$\mathcal{N}(0, 0.2)$')
plt.plot(x, y, label = '$\mathcal{y = 2x - 1}$')
plt.xlabel('$x$', fontsize = 13)
plt.ylabel('density: $p(x)$', fontsize = 13)
plt.title('Univariate normal distributions')
plt.ylim([0, 1])
plt.xlim([-3, 5])
plt.legend(loc = 1)
fig.subplots_adjust(bottom=0.15)
plt.show()
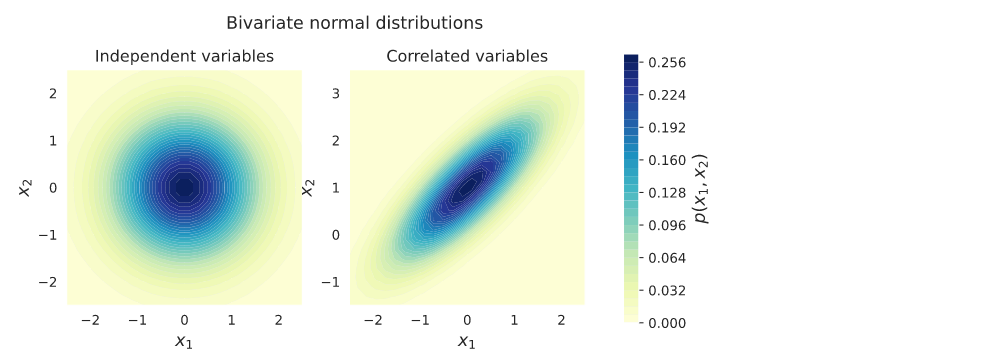
Multivariate normal distribution
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
def multivariate_normal(x, d, mean, covariance):
x_m = x - mean
return (1.0 / (np.sqrt( (2 * np.pi)**d * np.linalg.det(covariance)))) * np.exp(-0.5 * (np.linalg.solve(covariance, x_m).T.dot(x_m)))
# plot bivariate distribution
def generate_surface(mean, covariance, d):
# helper function to generate density surface
nb_of_x = 50
x1s = np.linspace(-5, 5, num=nb_of_x)
x2s = np.linspace(-5, 5, num=nb_of_x)
x1, x2 = np.meshgrid(x1s, x2s) # generate grid
pdf = np.zeros((nb_of_x, nb_of_x))
# file the cost matrix fro each combination of weights
for i in range(nb_of_x):
for j in range(nb_of_x):
pdf[i, j] = multivariate_normal(
np.matrix([[x1[i, j]], [x2[i,j]]]), d, mean, covariance)
return x1, x2, pdf
fig, (ax1, ax2) = plt.subplots(nrows = 1, ncols = 2, figsize = (8, 4))
d = 2
# plot of independent normals
bivariate_mean = np.matrix([[0.], [0.]]) # mean
bivariate_covariance = np.matrix([
[1.0, 0.0],
[0.0, 1.0]
])
x1, x2, p = generate_surface(bivariate_mean, bivariate_covariance, d)
con = ax1.contourf(x1, x2, p, 33, cmap=cm.YlGnBu)
ax1.set_xlabel('$x_1$', fontsize = 13)
ax1.set_ylabel('$x_2$', fontsize = 13)
ax1.axis([-2.5, 2.5, -2.5, 2.5])
ax1.set_aspect('equal')
ax1.set_title('Independent variables', fontsize = 12)
# Plot bivariate distribution
bivariate_mean = np.matrix([[0.], [1.]]) # mean
bivariate_covariance = np.matrix([
[1.0, 0.8],
[0.8, 1.0]
])
x1, x2, p = generate_surface(bivariate_mean, bivariate_covariance, d)
con = ax2.contourf(x1, x2, p, 33, cmap=cm.YlGnBu)
ax2.set_xlabel('$x_1$', fontsize = 13)
ax2.set_ylabel('$x_2$', fontsize = 13)
ax2.axis([-2.5, 2.5, -1.5, 3.5])
ax2.set_aspect('equal')
ax2.set_title('Correlated variables', fontsize = 12)
# add colorbar and title
fig.subplots_adjust(right = 0.8)
cbar_ax = fig.add_axes([0.85, 0.15, 0.02, 0.7])
cbar = fig.colorbar(con, cax = cbar_ax)
cbar.ax.set_ylabel('$p(x_1, x_2)$', fontsize = 13)
plt.suptitle('Bivariate normal distributions', fontsize = 13, y = 0.95)
plt.show()
Dirichlet distribution

Link tham khảo
Tài liệu tham khảo
Machine learning cơ bản
Hết.