Singular Value Decompostion
Các khái niệm cơ bản
Trị riêng và vector riêng
1
2
3
4
5
6
'''
A(n x n), lambda, x(n, ): A.x = lambda.x
--> lambda (tri rieng cua matrix A), x (vector rieng)
--> lambda khong am.
'''
print('formular 1')
Hệ trực giao và trực chuẩn
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
'''
Mot he co so U voi u_1, u_2, u_i (m, ) duoc goi "truc giao - orthogonal" if
+ cac vector u_i khac 0
+ tich cua 2 vector bang 0 (u_i.T * u_j = 0)
Mot he co so U voi u_1, u_2, u_m (m, ) duoc goi "truc chuan - orthonormal" if
+ no la mot he truc giao
+ norm2(u_i, u_j) = 1
Neu U truc chuan --> U * U.T = I (I: ma tran don vi bac m)
Luc nay, U goi la ma tran truc giao.
Tinh chat:
+ 1/U = U.T (nghich dao cua ma tran truc giao la chuyen vi cua no)
+ U la ma tran truc giao --> U.T cung la ma tran truc giao.
+ det(U) = 1 hoac -1
'''
print('formualar 2')
Cài đặt singular valued decompostion
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import numpy as np
from numpy import linalg as LA
m, n = 2, 3
A = np.random.rand(m, n)
# A(m, n) = U(mxm) * SUM_mt * V(mxn).T
U, S, V = LA.svd(A) # singular value decompostion
# U, V: ma tran truc giao
# U: U(mxm)
# S (cac phan tu o duong cheo cua ma trang SUM_mt)
# V: V(mxn).T
print('Frobenius norm of (U * U.T - I)', LA.norm(np.dot(U, U.T) - np.eye(m)))
print('\n', S, '\n')
print('Frobenius norm of (V * V.T - I)', LA.norm(np.dot(V, V.T) - np.eye(n)))
# U * U.T = I
# V * V.T = I
print(A)
B = np.dot(A, A.T)
print('\n', B)
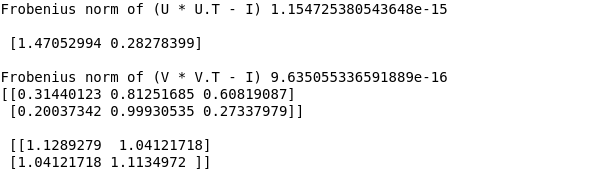
Image compresion
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
m, n = 1440, 960
# sinh ma tran gray_image
gray_image = np.random.rand(m, n)
from numpy import linalg as LA
U, S, V = LA.svd(gray_image)
def approx_rank_k(U, S, V, k = 4):
# matrix factorization using SVD
U_k = U[:, :k]
S_k = S[:k]
V_k = V[:k, :]
# dung lai ma tran gray_image
return np.around(U_k.dot(np.diag(S_k)).dot(V_k))
pre_gray_image = approx_rank_k(U, S, V)
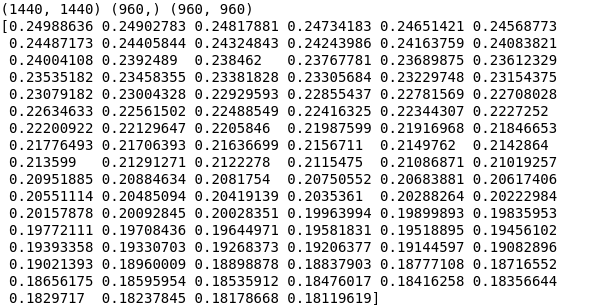
print(U.shape, S.shape, V.shape)
# Tinh do loi cua matrix sinh ra vs gray_image (error)
a = np.sum(S ** 2)
b = np.zeros_like(S)
for i in range(S.shape[0]):
b[i] = np.sum(S[:i+1] ** 2, axis = 0) / a
e = 1 - b
remain = gray_image - pre_gray_image
print(e[:100])
Link tham khảo
Tài liệu tham khảo
Machine learning cơ bản
Hết.