Gradient descent
cơ bản về đạo hàm, tối ưu xuống dốc
Import một số thư viện cần thiết
1
2
3
4
import math
import numpy as np
import matplotlib.pyplot as plt
# gradient descent (di nguoc) : GD
Hàm tính đạo hàm (auto)
1
2
3
''' Gradient Func (auto) '''
def gradient (f, x, epsilon = 1.0e-9):
return (f(x + epsilon/2) - f(x - epsilon/2)) / epsilon
Tính gradient descent theo công thức
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
'''f(x) = x^2 + 5sin(x)'''
epsilon = 1e-7
def cost(x):
return x ** 2 + 5 * np.sin(x)
def grad_manual(x):
return 2 * x + 5 * np.cos(x)
def myGD1(eta, x0): #x0: gia tri khoi tao ban dau
x = [x0]
for it in range(100):
x_new = x[-1] - eta * grad_manual(x[-1])
if(np.abs(grad_manual(x_new)) < epsilon):
break
x.append(x_new)
return (x, it)
def myGD2(eta, x0):
x = [x0]
for it in range(1000):
x_new = x[-1] - eta * gradient(cost, x[-1])
if(np.abs(gradient(cost, x[-1])) < epsilon):
break
x.append(x_new)
return (x, it)
(x1, it1) = myGD2(0.1, -5)
(x2, it2) = myGD2(0.1, 5)
print('myGD1: solution x1 = %f, cost = %f, after %d iterations' % (x1[-1], cost(x1[-1]), it1))
print('myGD1: solution x2 = %f, cost = %f, after %d iterations' % (x2[-1], cost(x2[-1]), it2))
(x1, it1) = myGD2(0.01, -5) # learning_rate eta (important)
(x2, it2) = myGD2(0.01, 5)
print('myGD2: solution x1 = %f, cost = %f, after %d iterations' % (x1[-1], cost(x1[-1]), it1))
print('myGD2: solution x2 = %f, cost = %f, after %d iterations' % (x2[-1], cost(x2[-1]), it2))

Một số hàm dùng để tối ưu GD (mommemtum, NAG)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
import numpy as np
import matplotlib.pyplot as plt
np.random.seed()
X = np.random.rand(1000, 1)
y = 4 + 3 * X + 0.2 * np.random.randn(1000, 1) # randn = random normal
print(X.shape)
print(y.shape)
one = np.ones((X.shape[0], 1))
Xbar = np.concatenate((one, X), axis = 1)
print(Xbar.shape)
# Loss function of Linear Regression
# np.linalg.norm: tinh norm
def cost(w): #w.shape(2, 1)
N = Xbar.shape[0]
return (0.5 / N) * np.linalg.norm(y - np.dot(Xbar, w), 2) ** 2
def grad_manual(w): #w.shape(2, 1)
N = Xbar.shape[0]
return (1.0 / N) * np.dot(Xbar.T, (np.dot(Xbar, w) - y))
# input w vector. w.shape = (2, )
def d_vec2vec(f, w, epsilon=1.0e-9): #w = [2, 1] --> (2, )
res = []
w = np.array(w, dtype=np.float64).reshape(-1, 1)
for i in range(w.shape[0]):
w_t = w.copy()
w_p = w.copy()
w_t[i] += epsilon / 2
w_p[i] -= epsilon / 2
res.append((f(w_t) - f(w_p)) / epsilon)
return np.concatenate(res, -1)
#input w: matrix and w.shape = Xbar.shape[1], y.shape[1]
def d_mt2mt(f, w, epsilon=1.0e-9): #w.shape (Xbar.shape[1], y.shape[1])
res = np.zeros_like(w)
for i in range(w.shape[0]):
w_t = w.copy()
w_p = w.copy()
w_t[i] += epsilon / 2
w_p[i] -= epsilon / 2
res[i] = (f(w_t) - f(w_p)) / epsilon
return res
#test
w_init = np.array([[2], [1]]) # 2x1
w_init1 = np.array([[1, 2]]) # 1x2
w = np.random.rand(Xbar.shape[1], y.shape[1])
print(w)
print(grad_manual(w))
print(d_mt2mt(cost, w))
def myGD(w_init, grad, eta = 1):
w = [w_init]
for it in range(10000):
w_new = w[-1] - eta * grad(w[-1])
#norm1 == abs
if np.linalg.norm(grad(w_new)) / len(w_new) < epsilon:
break
w.append(w_new)
return (w, it)
#toi uu (local minimum vs global minumum)
def myGD_momentum(w_init, grad, eta, gamma):
w = [w_init]
v = [np.zeros_like(w_init)]
for it in range(10000):
v_new = gamma * v[-1] + eta*grad(w[-1])
w_new = w[-1] - v_new
if np.linalg.norm(grad(w_new)) / len(w_new) < epsilon:
break
w.append(w_new)
v.append(v_new)
return (w, it)
# optimal nesterov accelerated gradient (NAG)
def myGD_NAG(w_init, grad, eta, gamma):
w = [w_init]
v = [np.zeros_like(w_init)]
for it in range(10000):
v_new = gamma * v[-1] + eta * grad(w[-1] - gamma*v[-1])
w_new = w[-1] - v_new
if np.linalg.norm(grad(w_new)) / len(w_new) < epsilon:
break
w.append(w_new)
v.append(v_new)
return (w, it)
def myGD2(w_init, grad, eta = 1):
w = [w_init]
for it in range(10000):
w_new = w[-1] - eta * d_mt2mt(cost, w[-1])
if np.linalg.norm(d_mt2mt(cost, w[-1])) / len(w_new) < epsilon:
break
w.append(w_new)
return (w, it)
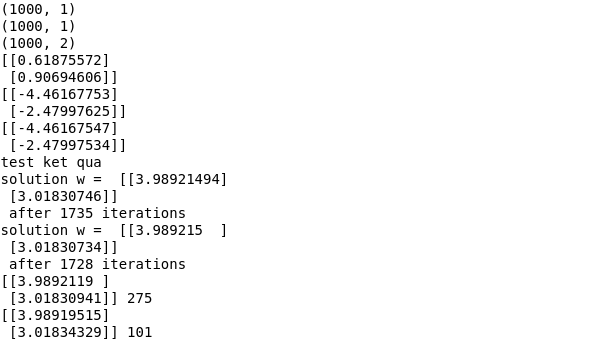
print('test ket qua')
(w1, it1) = myGD(w, grad_manual, 0.1)
print('solution w = ', w1[-1], '\n after %d iterations' % (it1 + 1))
(w2, it2) = myGD2(w, d_mt2mt, 0.1)
print('solution w = ', w2[-1], '\n after %d iterations' % (it2 + 1))
(w_mm, it_mm) = myGD_momentum(w, grad_manual, 0.5, 0.9)
print(w_mm[-1], it_mm)
(w_nag, it_nag) = myGD_NAG(w, grad_manual, 0.5, 0.9)
print(w_nag[-1], it_nag)
Stochastic Gradient Descent
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#Batch Gradient Descent (tinh dao ham cua ham mat mat all data)
'''
Stochastic Gradient Descent
tinh dao ham cua ham mat mat tai 1 diem
co the ap dung cac thuat toan tang toc momemtum, adagrad,...
'''
# tinh single point gradient
def sgrad_manual(w, i, random_id):
true_i = random_id[i]
xi = Xbar[true_i, :]
yi = y[true_i]
a = np.dot(xi, w) - yi
return (xi * a).reshape(2, 1)
def SGD(w_init, eta):
w = [w_init]
w_last_check = w_init
iter_check_w = 10
N = Xbar.shape[0]
count = 0
for it in range(10):
#shuffle data
random_id = np.random.permutation(N)
for i in range(N):
count += 1
g = sgrad_manual(w[-1], i, random_id)
w_new = w[-1] - eta * g
w.append(w_new)
if count % iter_check_w == 0:
w_this_check = w_new
if np.linalg.norm(w_this_check - w_last_check) / len(w_init) < epsilon:
return w
w_last_check = w_this_check
return w
w_sgd = SGD(w, 0.1)
print(w_sgd[-1])

Lưu ý
1
2
# khac voi SGD, Mini-batch gradient descent su dung
# so luong n > 1 va n << N (thuong n = 50 - 100)
Link tham khảo
Tài liệu tham khảo
Machine learning cơ bản
Hết.