Mạng neuron nhân tạo và ứng dụng
Tìm hiểu về kiến trúc và cách cài đặt mạng neuron
Kiến trúc mạng neuron
Giới thiệu kiến trúc và ký hiệu của mạng neuron
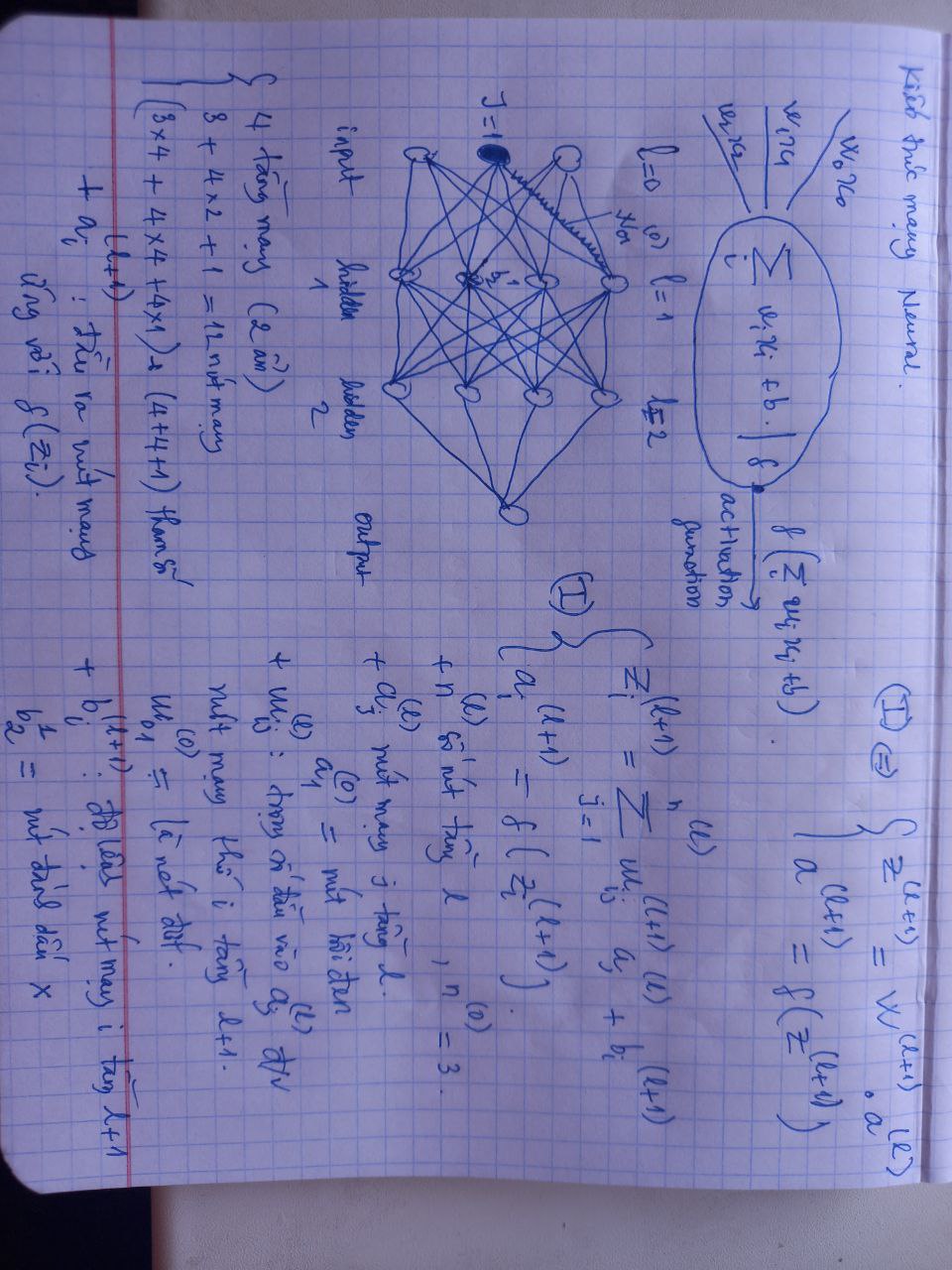
Cách tính đạo hàm tiến (feedforward) và lan truyền ngược (back propagation)
Công thức tính đạo hàm tiến và cách thực hiện lan truyền ngược

Hàm lỗi và chứng minh đạo hàm
Hàm lỗi và chứng minh chi tiết đạo hàm của lan truyền ngược

Ứng dụng vào bài toán MNIST
Load dữ liệu của bài toán
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
import os
import gzip
import pickle
import numpy as np
import urllib3
DATA_FILE = 'mnist.pkl.gz'
def download():
# download MNIST dataset
url = 'https://github.com/mnielsen/neural-networks-and-deep-learning/raw/master/data/mnist.pkl.gz'
http = urllib3.PoolManager()
r = http.request('GET', url, preload_content = False)
with open(DATA_FILE, 'wb') as out:
while True:
data = r.read(4096)
if not data:
break
out.write(data)
r.release_conn()
print('downloaded!')
# one hot label [1 2 3 4 5 6 7 8 9 10]
# chuyen thanh vector nhi phan tai position = 1
def label_2_vec(label):
v = np.zeros((10, 1))
v[label] = 1.0
return v
def load():
if not os.path.exists(DATA_FILE):
download()
with gzip.open(DATA_FILE, 'rb') as file:
tr_dt, v_dt, t_dt = pickle.load(file, encoding='iso-8859-1')
# training data
inputs = [x.reshape((784, 1)) for x in tr_dt[0]]
labels = [label_2_vec(y) for y in tr_dt[1]]
training_data = zip(inputs, labels)
# validataion data
inputs = [x.reshape((784, 1)) for x in v_dt[0]]
validation_data = zip(inputs, v_dt[1])
# test data
inputs = [x.reshape((784, 1)) for x in t_dt[0]]
test_data = zip(inputs, t_dt[1])
return (training_data, validation_data, test_data)
Đọc dữ liệu và kiếm tra việc sinh ma trận trọng số (w)
1
2
3
4
5
6
7
8
9
10
training_data, validation_data, test_data = load()
training_data = list(training_data)
validataion_data = list(validation_data)
test_data = list(test_data)
# test sinh ma tran w
layers = [784, 100, 200, 10]
for l2, l1 in zip(layers[1:], layers[:-1]):
print(l2, l1)
Xây dựng class Mạng neural
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
import time
import random
class NN():
def __init__(self, layers):
# layers = [784, 100, 200, 10]
self.layers = layers
self.L = len(layers)
self.w = [np.random.randn(l2, l1 + 1) for l2, l1 in zip(layers[1:], layers[:-1])]
#w[0] = (100, 785), 1 cot la bias
#w[1] = (200, 101) # trong so doi voi tang 2
#w[2] = (10, 201) # trong so doi voi tang 3
def feedforward(self, x): #x: 1 buc anh.
z = []
a = [self.add_bias(x)] # a0 = x
for l in range(1, self.L):
#l = [0, 1, 2, 3]
#w[0] la trong so doi voi tang 1
z_l = np.dot(self.w[l-1], a[l-1])
a_l = self.sigmoid(z_l)
if l < self.L - 1:
a_l = self.add_bias(a_l) # add bias doi voi tang (khac cuoi cung)
z.append(z_l)
a.append(a_l)
return (z, a)
def predict(self, x):
_, a = self.feedforward(x)
return np.argmax(a[-1])
def add_bias(self, a):
# a = [784, 1]
# after add_bias --> [785, 1] voi a[0] = 1
return np.insert(a, 0, 1, axis = 0)
def sigmoid(self, z):
# sigmoid function use as activation function
return 1.0 / (1.0 + np.exp(-z))
def cost(self, data):
# return cross-entropy cost of NN on test data
m = len(data)
j = 0
for x, y in data:
# x: (784, 1)
# y: label (ex: 7)
_, a = self.feedforward(x)
a_L = a[-1]
j += np.sum(np.nan_to_num(y * np.log(a_L) + (1 - y) * np.log(1 - a_L)))
return -j / m
def evaluate(self, test_data):
results = [(self.predict(x), y) for (x, y) in test_data]
return sum(int(_y == y) for (_y, y) in results)
def backprop(self, x, y):
# backpropagation to calc derivatives
w_grad = [np.zeros(W.shape) for W in self.w]
#feedforward
z, a = self.feedforward(x)
#backward
dz = a[-1] - y # da chung minh o hinh viet.
for _l in range(1, self.L):
l = -_l # layer index
if l < -1:
#da = a[l] * (1 - a[l])
da = self.sigmoid_grad(z[l])
# do not calc for w_0 (da_0 /dz = 0 because a_0 = 1 for all z)
dz = np.dot(self.w[l+1][:, 1:].transpose(), dz) * da
# gradient
w_grad[l] = np.dot(dz, a[l-1].transpose())
return w_grad
def sigmoid_grad(self, z):
s = self.sigmoid(z)
return s * (1 - s)
def train(self, train_data, epochs, mini_batch_size, eta):
# train NN with train data
# use mini-batch SGD method to train the NN
m = len(train_data)
# cost
cost = []
for j in range(epochs):
start_time = time.time()
#shuffle data before run
random.shuffle(train_data)
#divide data into mini batchs
for k in range(0, m, mini_batch_size):
mini_batch = train_data[k : k + mini_batch_size]
m_batch = len(mini_batch)
# calc gradient
w_grad = [np.zeros(W.shape) for W in self.w]
for x, y in mini_batch:
grad = self.backprop(x, y)
w_grad = [W_grad + g for W_grad, g in zip(w_grad, grad)]
w_grad = [W_grad / m_batch for W_grad in w_grad]
#update w
self.w = [W - eta * W_grad for W, W_grad in zip(self.w, w_grad)]
# calc cost
cost.append(self.cost(train_data))
return cost
Test và đánh giá mô hình
Sử dụng 1 lớp ẩn
1
2
3
4
5
nn = NN([784, 100, 10])
nn.train(training_data, 30, 100, 3.0)
correct = nn.evaluate(test_data)
total = len(test_data)
print(correct, total, 100.0 * correct / total)
Hoặc sử dụng 2 lớp ẩn
1
2
3
4
5
nn = NN([784, 100, 200, 10])
nn.train(training_data, 30, 100, 3.0)
correct = nn.evaluate(test_data)
total = len(test_data)
print(correct, total, 100.0 * correct / total)
Link tham khảo
Tài liệu tham khảo
Machine learning cơ bản
Hết.