Một số ký hiệu cơ bản trong markdown
Tổng hợp một số ký hiệu cơ bản dùng trong markdown và biểu diễn một số công thức để viết toán học.
Ipython3
import matplotlib.pyplot as plt
# Create outlier in 2002-05
df.loc["2002-05"]["Sales"] = df.loc["2002-05"]["Sales"]+500
plt.figure(figsize=(10, 6))
plt.plot(df["Sales"], marker="o")
plt.xticks(rotation=45)
plt.xlabel("Time", fontsize=12)
plt.ylabel("Shampoo revenue", fontsize=12)
plt.title("Shampoo revenue in three years", fontsize=18)
plt.show()
Python
1
2
3
4
5
6
7
8
9
10
def d_vec2vec(f, w, epsilon=1.0e-9):
res = []
w = np.array(w, dtype=np.float64).reshape(-1, 1)
for i in range(w.shape[0]):
w_t = w.copy()
w_p = w.copy()
w_t[i] += epsilon / 2
w_p[i] -= epsilon / 2
res.append((f(w_t) - f(w_p)) / epsilon)
return np.concatenate(res, -1)
Viết theo bảng
| Cú pháp | Mô tả |
|---|---|
| row1 | mô tả gì đó |
| row2 | mô tả cho hàng thứ 2 |
import torch
# Khởi tạo ma trận A kích thước m, n, p = 2, 3, 4
A = torch.randn([2, 3, 4])
# Truy cập ma trận đầu tiên
A[:1, :, :]
Một vài công thức toán
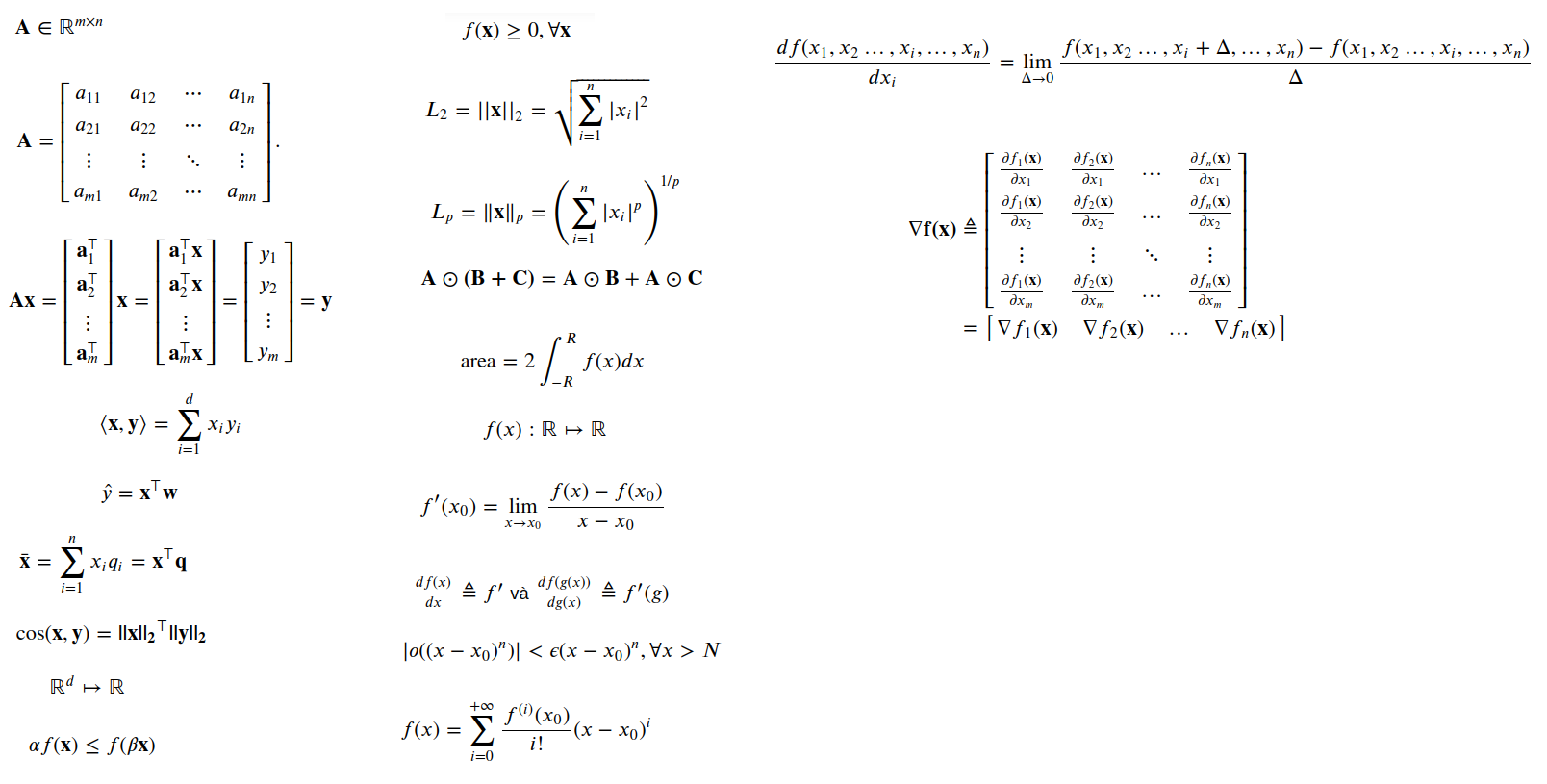
$\mathbf{A} \in \mathbb{R}^{m\times n}$
\mathbf{A}: chữ A đậm
\in: dấu thuộc tập hợp
\mathbb{R}: chữ R to rỗng
^: mũ
\time: dấu nhân (x)
$$\begin{split}\mathbf{A}=\begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m1} & a_{m2} & \cdots & a_{mn} \\
\end{bmatrix}.\end{split}$$
\begin{split}: viết ở giữa
\begin{bmatrix} : ma trận
a_{11}: chỉ số xuống (viết nhỏ)
&: thêm dấu cách vào
\cdots: 3 chấm ngang
\vdots: 3 chấm đứng
\ddots: 3 chấm chéo.
$$\mathbf{A}\mathbf{x} =
\begin{bmatrix}
\mathbf{a}^\top_{1} \\
\mathbf{a}^\top_{2} \\
\vdots \\
\mathbf{a}^\top_m \\
\end{bmatrix} \mathbf{x} = \begin{bmatrix}
\mathbf{a}^\top_{1} \mathbf{x} \\
\mathbf{a}^\top_{2} \mathbf{x} \\
\vdots \\
\mathbf{a}^\top_m \mathbf{x} \\
\end{bmatrix} = \begin{bmatrix}
y_1 \\
y_2 \\
\vdots \\
y_m
\end{bmatrix} = \mathbf{y}$$
\begin{split}: viết ở giữa
\begin{bmatrix} : ma trận
a_{11}: chỉ số xuống (viết nhỏ)
&: thêm dấu cách vào
\cdots: 3 chấm ngang
\vdots: 3 chấm đứng
\ddots: 3 chấm chéo.
$$\langle \mathbf{x}, \mathbf{y} \rangle = \sum_{i=1}^{d} x_i y_i$$
\langle: dấu mở (<)
\rangle: dấu đóng (>)
sum_{i=1}^{d}: i = 1 ở phía dưới, d ở phía trên
$$\hat{y} = \mathbf{x}^{\top}\mathbf{w}$$
\hat{y}: y mũ
{\top}: ký hiệu T
$$\bar{\mathbf{x}} = \sum_{i=1}^{n} x_i q_i= \mathbf{x}^{\top}\mathbf{q}$$
\bar: giá trị trung trình
$\cos({\mathbf{x}, \mathbf{y}}) = \mathbf{||x||_2}^{\top}\mathbf{||y||_2}$
x_2: trị tuyệt đối của x
$\mathbb{R}^{d} \mapsto \mathbb{R}$
\mapsto: dấu mũi tên ->
1 shift 4: viết công thức trực tiếp
2 shift 4: viết công thức ở giữa.
$\alpha f(\mathbf{x}) \leq f(\beta\mathbf{x})$
alpha, beta: các giá trị của biến
\leq: dấu nhỏ hơn
$f(\mathbf{x}) \geq 0, \forall \mathbf{x}$
\geq: lớn hơn hoặc bằng
\forall: với mọi
$$L_{2} = ||\mathbf{x}||_2 = \sqrt{\sum_{i=1}^n |x_i|^2 }$$
sqrt: căn bậc 2
$$L_{p} = \|\mathbf{x}\|_p = \left(\sum_{i=1}^n \left|x_i \right|^p \right)^{1/p}$$
\left(: Mở ngoặc (
\right): Đóng ngoặc )
$\mathbf{A} \odot \mathbf{(B+C)} = \mathbf{A} \odot \mathbf{B} + \mathbf{A} \odot \mathbf{C}$
\odot: dấu tròn chấm lớn
$$\text{area} = 2\int_{-R}^{R} f(x) dx$$
\text {}: text bình thường
\int_{-R}^{R}: tích phân từ -R đến R.
$f(x) : \mathbb{R} \mapsto \mathbb{R}$
đã biết
$$f'(x_0)= \lim_{x \rightarrow x_0}\frac{f(x)-f(x_0)}{x-x_0} \tag{1}$$
\lim_{x \rightarrow x_0}: lim của x tiến đến x0
\rightarrow: dấu mũi tên
\frac{f(x)-f(x_0)}{x-x_0}: phân số tử chia cho mẫu
\tag{1}: ghi chú công thức là số (1)
$\frac{d f(x)}{d x} \triangleq f'$ và $\frac{d f(g(x))}{d g(x)} \triangleq f'(g)$
\triangleq: tam giác trên dấu bằng
$$|o((x-x_0)^n)| < \epsilon (x-x_0)^n, \forall x > N$$
\epsilon: giá trị epsilon
$$f(x) = \sum_{i=0}^{+\infty} \frac{f^{(i)}(x_0)}{i!}(x-x_0)^i$$
\infty: vô cùng
$$\frac{d f(x_1, x_2 \dots, x_i, \dots, x_n)}{d x_i} = \lim_{\Delta \rightarrow 0} \frac{f(x_1, x_2 \dots, x_i+\Delta, \dots, x_n)- f(x_1, x_2 \dots, x_i, \dots, x_n)}{\Delta}$$
\dots: dấu 3 chấm
\Delta: hình tam giác (biểu diễn ký hiện delta)
$$\begin{eqnarray}
\nabla \mathbf{f(x)} &\triangleq &
\left[
\begin{matrix}
\frac{\partial f_1(\mathbf{x})}{\partial x_1} & \frac{\partial f_2(\mathbf{x})}{\partial x_1} & \dots & \frac{\partial f_n(\mathbf{x})}{\partial x_1} \\
\frac{\partial f_1(\mathbf{x})}{\partial x_2} & \frac{\partial f_2(\mathbf{x})}{\partial x_2} & \dots & \frac{\partial f_n(\mathbf{x})}{\partial x_2} \\
\vdots & \vdots & \ddots & \vdots \\
\frac{\partial f_1(\mathbf{x})}{\partial x_m} & \frac{\partial f_2(\mathbf{x})}{\partial x_m} & \dots & \frac{\partial f_n(\mathbf{x})}{\partial x_m}
\end{matrix}
\right] \\
& = &
\left[
\begin{matrix}
\nabla f_1(\mathbf{x}) & \nabla f_2(\mathbf{x}) & \dots & \nabla f_n(\mathbf{x})
\end{matrix} \right]
\end{eqnarray}$$
\nabla : tam giác ngược
&\triangleq: tam giác trên dấu bằng
\left[: ký hiệu mở vuông bên trái
\partial: đạo hàm từng phần
& : dấu cách
Hình ảnh công thức minh họa
Link tham chiếu
Hết!